Bewegungsmuster
Felix Malte Schneppe
Wie in jedem guten gegnerbasierten Spiel, sollen die Gegner weder auf der Stelle bleiben noch sich zu vorausschauend verhalten. Ziel ist es daher, den Gegner ein intelligentes Bewegungsverhalten mitzugeben, welches sowohl schnell kalkulierbar als auch natürlich ist. Hierbei muss darauf geachtet werden, dass für den Spieler die Gegner nicht unbesiegbar werden, sondern ein angemessenes Verhältnis zwischen dem Verkommen zu einer Zielscheibe und taktischem Vorgehen gewahrt wird.
Bei der Bewegung geht jeder Gegner in jedem render-Durchlauf durch die folgenden vier Schritte:
- Bestimme eine optimale Richtung
- Sammel mögliche Hindernisse auf diesem Weg
- Berechne eine neue Richtung, die diesen ausweicht
- Aktualisiere alle Gegnerinformationen
Zu 4. gehört unter anderem das richtige Drehen des Schiffs, sodass es sich nicht nur in Flugrichtung bewegt, sondern auch blickt.
if(this.direction.length() == 0) {
// do nothing
} else {
dir.normalize();
var viewDir = this.position.clone();
dir.multiplyScalar(10 * this.speed)
viewDir.add(dir);
this.lookAt(viewDir);
...
}
Liegt in den nächsten Sekunden des Flugs kein Objekt auf der Flugstrecke, so bewegt sich der Gegner auf den Spieler zu. Existieren Hindernisse, so soll der Abstand zwischen Spieler und Gegner minimiert werden, jedoch ein hinreichend großer Abstand zu allen Objekten eingehalten werden. Dies führt zum Optimierungsproblem
für ein reelles C. Das Lösen dieses Problems ist komplex, sodass eine hohe Framerate nicht mehr gesichert wäre. Deshalb nutzen die Gegner andere Ausweichstrategien.
Ausweichen
Um das Spiel realistisch zu halten, sollten die Gegner den gesammelten Hindernissen ausweichen. Daher wird eine Ausweichrichtung gesucht, die je nach Algorithmus die neue Flugrichtung darstellt oder der optimalen Richtung hinzuaddiert wird. Beim Suchen einer Ausweichrichtung unterscheidet jeder Gegner nach der Anzahl der um ihn befindlichen Hindernisse.
Ausweichen bei einem Hindernis
Für ein Hindernis in der Umgebung des Gegners wird eine Ausweichrichtung (siehe avoidObstacle) sehr explizit mit Hilfe von linearen Gleichungen bestimmt.
Ein Spezialfall stellt die anbahnende Kollision mit einem Asteroiden oder Partner dar. Bewegt sich ein Objekt nahezu entgegengesetzt zur Flugbahn des Gegners, besteht die Gefahr einer Kollision. Um dies zu verhindern, weicht der Gegner so schräg wie möglich aus und entgeht somit dem Aufeinandertreffen.
Die anderen beiden Fälle werden simultan behandelt. Bewegt sich ein Objekt nicht auf einen zu, so kann es entweder in der bevorzugten Flugbahn liegen oder sich außerhalb dieser bewegen. Eine einfache Möglichkeit stellt die Bewegung entgegengesetzt zur Flugrichtung des Hindernisses dar, welche sich allerdings als nicht praktikabel erwies.
// weiche aus in Richtung der Normalen des Schnittpunkts
dir = optimalDir.clone();
// Berechne t (Minimierer des Abstands)
var t = obstacle.position.clone();
t.sub(this.position);
t.dot(dir);
t.divideScalar(dir.lengthSq());
// Berechne Minimum
dir.multiplyScalar(t);
dir.add(this.position);
// Falls getroffen
if(dir.distanceTo(obstacle.position) < obstacle.radius) {
avoidDir = dir;
avoidDir.sub(obstacle.position);
} else {
// Falls nicht in Richtung
avoidDir = new THREE.Vector3(
this.position.x - obstacles[0].position.x,
this.position.y - obstacles[0].position.y ,
this.position.z - obstacles[0].position.z);
avoidDir.normalize();
}
Liegt das Hindernis auf Kollisionskurs, so berechnet der Algorithmus den Punkt auf der Geraden der optimalen Richtung, der dem Mittelpunkt des Objekts am nächsten kommt. Ausgehend von diesem Punkt wird dann in diese Richtung (vom Hindernis gesehen) ausgewichen. Idee ist hierbei, orthogonal zur Idealrichtung auszuweichen.
Auch ohne bevorstehende Kollison sollte sich der Gegner vom Hindernis wegbewegen, allerdings genügt hier ein kleinerer Einfluss, der durch die Richtung der zum Spieler zeigenden Normalen der Sicherheitskugel erreicht wird.
Durch die Gewichtung wird ein Zusammenprall verhindert.
// Gewichte die Laengen, um Kollision zu vermeiden
var bestImpact = this.position.distanceTo(obstacles[0].position);
var avoidImpact = 1.5 * maxAsteroidSize;
avoidDir.multiplyScalar(avoidImpact);
dir = optimalDir.clone();
dir.multiplyScalar(bestImpact);
dir.add(avoidDir);
Diese Strategie hat den Nachteil, dass es bei mehreren Hindernissen zu Auslöschungen der linearen Ausweichrichtungen kommt. Deshalb setzen die Gegner dort auf eine andere Strategie.
Ausweichen bei mehreren Hindernissen
Die Idee fürs Suchen einer Ausweichrichtung bei mehreren Objekten in direkter Umgebung ist relativ simpel. Generell durchsucht der Algorithmus hinter avoidObstacles den Raum systematisch nach einer geeigneten Flugrichtung. Ausnahme stellt hierbei der Spezialfall dar, dass der Weg zum Spieler nicht direkt versperrt wird. Dann behält das Schiff seine angestrebte Richtung bei.
Unter der Voraussetzung, dass möglichst gering vom angestrebten Weg abgewichen wird, sitzt der Saatpunkt des Algorithmus' bei der optimalen Richtung. Um das Rechnen zu vereinfachen betrachten wir die Szene durch eine in einem gewissen Abstand (this.speed x delta) aufgespannte Leinwand. Die Gegnerschiffe dürfen nur im Ausnahmefall orthogonal fliegen. In allen anderen Fällen sollen sie einen maximalen Flugwinkel von hier 70° nicht überschreiten.
var scalar = this.speed * delta * Math.tan(maxShipAngle); // Hoehe der Plane
var checkingDistance = 0.2 * scalar; // da 6 Iterationen
var tmp = obstacles.length;
var collisions = [tmp,tmp,tmp,tmp];
// setze die Laengen von U und V neu, auf maximale Distanz
// (je nach Winkel des Raumschiffs)
UVN = this.getUVN(optimalDir);
var U = UVN[0];
var V = UVN[1];
U.multiplyScalar(checkingDistance);
V.multiplyScalar(checkingDistance);
avoidObstacles durchsucht nun auf dieser Leinwand in der ersten Iteration vier nebenliegende Eckpunkte. Unter diesen sucht er sich die Richtung aus, die am wenigsten mögliche Kollisionen zählt. Dies errechnet checkDirection. Sollte eine Richtung gefunden sein, die kein Hindernis aufweist, so wird die Flag directionFound = true gesetzt. Andernfalls wird um die Richtung, die im letzten Durchgang am wenigsten Hindernisse aufwies mit demselben Algorithmus ein Kandidat gesucht. Dieser Algorithmus wird bis zu fünfmal in einer kleineren Umgebung wiederholt. Wird ein geeigneter Kandidat gefunden, so soll vermieden werden, dass sich der Gegner in Richtung eines "Nadelöhrs" begibt. Daher wird zum Validieren ein weiteres Mal iteriert und eine Richtung erst dann als gültig erklärt, wenn auch hier keine Hindernisse angeflogen werden. Andernfalls wird ausgehend von der beobachteten Richtung weiter iteriert.
Ausnahme ist der letzte Durchlauf. Da eine weitere Validierung in den anderen Strategien ebenfalls nicht vorkommt, genügt auch hier das reine Finden eines Kandidaten.
Ist der Algorithmus nicht erfolgreich, so wird fünfmal versucht, per Zufall eine mögliche Richtung auf der Leinwand zu erraten. Gelingt auch dies nicht, werden deren Eckpunkte betrachtet. Im seltenen Fall reicht auch dies nicht aus, sodass sich der Gegner ausnahmsweise orthogonal zur optimalen Richtung bewegen darf. Sollte auch dieser Weg versperrt, also der Gegner regelrecht umzingelt sein, so bleibt ihm nichts anderes übrig, als stehen zu bleiben und zu hoffen, dass sich die Situation auflöst.
Validieren einer Richtung
Nach jedem Versuch des Findens einer neuen Richtung, muss diese überprüft werden. Dabei stellen wir uns Kugeln mit einem etwas größeren Radius um jedes Objekt vor, als es groß ist. Dies stellt sicher, dass wir einen ausreichenden Sicherheitsabstand zum Hindernis halten. Hierfür könnte man um jedes Objekt eine SphereGeometry legen und diese mit einem Raycaster durchschießen. Obwohl dies der von Three.js geplante Weg ist, stellt der hohe Rechenaufwand ein Problem dar.
Stattdessen suchen wir das Minimum der Distanz zwischen der Geraden vom Gegnerschiff in die zu validierende Richtung und jedem der möglichen Hindernisse:
Einsetzen des s liefert die minimale Distanz. Ist diese zu klein, ist die Wahrscheinlichkeit hoch zu kollidieren, weshalb der Hinderniszähler count inkrementiert wird.
// Ueberprueft die Richtung auf Hindernisse
// @return #Hindernisse
Enemy.prototype.checkDirection = function(direction, objects) {
var count = 0;
for(obj of objects) {
// Berechne t (Minimierer des Abstands)
var t = obj.position.clone();
t.sub(this.position);
t.dot(direction);
t.divideScalar(direction.lengthSq());
// Berechne Minimum
direction.multiplyScalar(t);
direction.add(this.position);
// Wie nahe dran
if(direction.distanceTo(obj.position) < 1.2 * obj.radius) {
count += 1;
}
}
return count;
}
Bewegung in Spielernähe
In direkter Spielernähe soll sich der Gegner taktisch so klug verhalten, dass er weder zu leicht noch zu schwer zu treffen ist. Insbesondere soll er keinen Kamikazeangriff starten, sondern auch sein eigenes Überleben sichern. Hierbei ist zu beobachten, dass eine Position hinter dem Spieler sowohl fürs eigene Überleben als auch für die eigenen Angriffsbestrebungen förderlich ist. Dies nutzen wir, um eine solche Position über den Flug auf einer Kurve zu erreichen.
Three.js bietet verschiedene Möglichkeiten, Kurven zu spezifizieren. Als für unsere Anwendung passabel stellten sich der Einsatz von Bezierkurven sowie von Splines dar. Da wir vor allem verhindern wollten, dass es zwischen dem Spieler und einem der Gegner zur Kollision kommt, haben wir uns für die interpolierende Kurve, dem Spline, entschieden. Aufgehängt haben wir diesen an vier Eckpunkten. Der Startpunkt ist hierbei immer unser jetziger Standort. Der Endpunkt wird immer durch die aktuelle Spielerposition beschrieben.
Aus dem Blickfeld des Spielers gelangen
Ist der Gegner vor dem Spieler platziert, sinken seine Überlebenschancen rapide. Daher ist er gewollt, hinter dem Spieler zu gelangen.
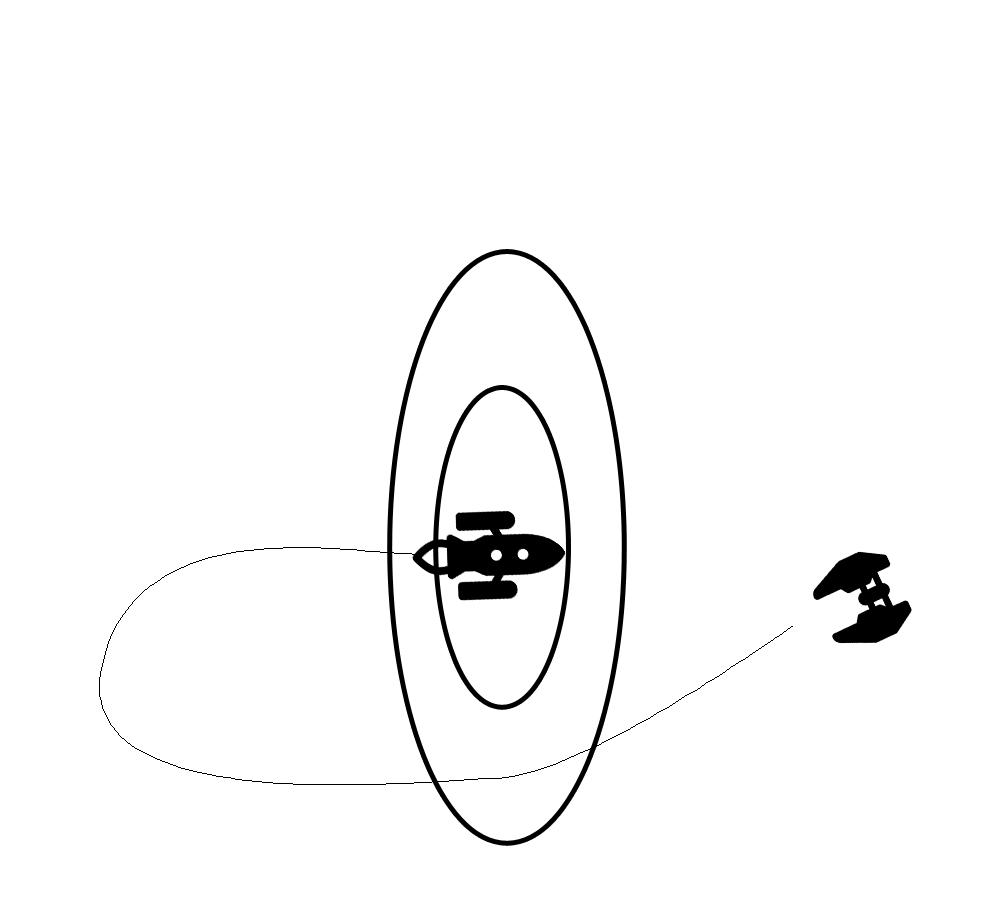
Hierfür haben wir zuzüglich zur aktuellen sowie zur Spielerposition zwei Punkte, die wir frei spezifizieren können.
Als erste Bedingung gilt dabei, dass eine Kollision mit dem Spieler möglichst vermieden werden sollte. Daher bewegt sich der Spieler in Richtung eines auf einem Kreisbogen liegenden Punkts. Dieser Kreisbogen liegt dabei auf der orthogonal zur Richtung des Gegners zum Spieler liegenden Ebene.
Der zweite Punkt liegt um die halbe Distanz zwischen Gegnerschiff und Spielerschiff weiter nach hinten versetzt und tendenziell dichter an der Geraden N, die durch die beiden Schiffe verläuft.
var N = ship.position.clone();
N.sub(this.position);
// orthogonale Vektoren, um Plane aufzuspannen
var U = N.clone();
U.cross(new THREE.Vector3(0,1,0));
var V = U.clone();
V.cross(N);
U.normalize();
V.normalize();
....
p1 = ship.position.clone();
p1.add(U.multiplyScalar(2*(shipSize + Math.random() * shipSize)));
p1.add(V.multiplyScalar(2*(shipSize + Math.random() * shipSize)));
U.normalize();
V.normalize();
p2 = ship.position.clone();
p2.add(N.multiplyScalar(1.5));
p2.add(U.multiplyScalar(Math.random() * 2 * (shipSize + Math.random() * shipSize)));
p2.add(V.multiplyScalar(Math.random() * 2 * (shipSize + Math.random() * shipSize)));
Dem Spieler folgen
Für den Angreifer ist die Position hinter dem Spieler förderlich. Er selber hat sein Ziel im Auge und ist dennoch außerhalb der Sichtweite des Rivalen. Um selbst bei einer höheren Geschwindigkeit nicht auf diesen aufzulaufen oder ihn gar zu überholen, dreht der Gegner daher eine Schleife. So kann er seine günstige Position wahren.
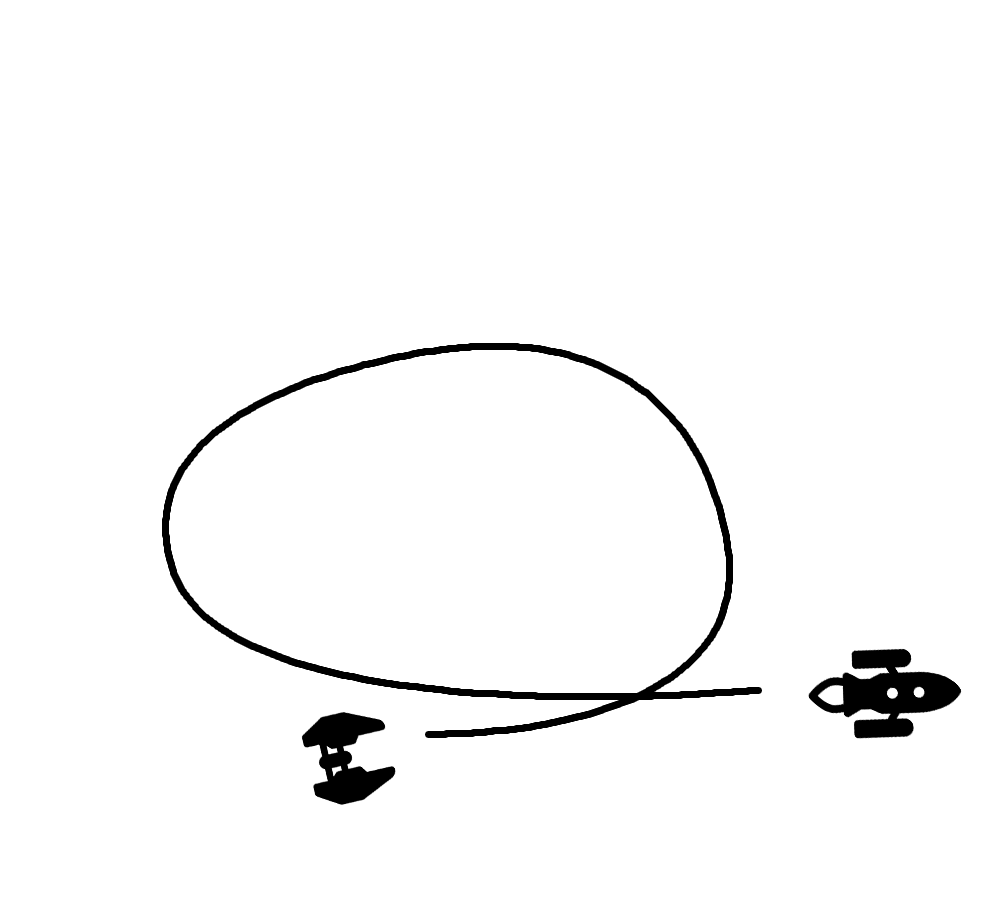Wie beim obigen Algorithmus werden auch hier zwei weitere Wegpunkte der Kurve gesetzt. Der erste Wegpunkt verkürzt dabei die Distanz auf ein Drittel der ursprünglichen, verschiebt sich dann allerdings noch orthogonal. Danach geht es für den Gegner doppelt so weit wieder nach hinten, bevor er sich wieder in Richtung des Spielers und Rivalens orientiert.
p1 = this.position.clone();
p1.add(N.multiplyScalar(2/3));
p1.add(U.multiplyScalar(2 * (shipSize + Math.random() * shipSize)));
p1.add(V.multiplyScalar(2 * (shipSize + Math.random() * shipSize)));
U.normalize();
V.normalize();
N.multiplyScalar(3/2);
p2 = this.position.clone();
p2.add(N.multiplyScalar(-2/3));
p2.add(U.multiplyScalar(2 * (shipSize + Math.random() * shipSize)));
p2.add(V.multiplyScalar(2 * (shipSize + Math.random() * shipSize)));
Mithilfe des CatmullRom-Algorithmus wird dann die Kurve erzeugt.
var curve = new THREE.CatmullRomCurve3([
this.position.clone(),
p1,
p2,
ship.position.clone()]);
Um nicht während des Wendemanövers zu einem einfachen Ziel zu werden, achten die Gegner auf die Flugbahn des Spielers und berechnen eine neue Flugtaktik, sobald sich der Spieler um mehr als 90° zur ursprünglichen Richtung gedreht hat.
var renew = false;
// Falls Spieler umgedreht (im Vergleich zum initialisieren), neu machen
if(this.oldPlayerDir.dot(this.playerDirection) < 0) {
renew = true;
}
Auch während des Wendens können Asteroiden und Verbündete zur Gefahr werden. Die allgemein gehaltene Variable optimalDir kommt dabei allerdings zum Tragen. Statt die Kurve exakt nachzufliegen, entnehmen wir ihr nur ein paar Punkte auf der Strecke, die als nächstes Ziel gelten. Die Anzahl der anzufliegenden Punkte richtet sich dabei nach der Aufruffrequenz, der Geschwindigkeit des Schiffs sowie der Länge der Kurve. Allgemein gelten folgende Beziehungen:
- Je länger die Kurve, desto mehr Punkte müssen abgelaufen werden.
- Je höher die Geschwindigkeit, desto weniger Punkte müssen abgelaufen werden.
- Je größer das delta, desto weiter kann sich der Gegner in einem Durchlauf bewegen. Daher müssen weniger Punkte abgelaufen werden.
Als Proportionalitätskonstante hat sich die Wahl von 1/2 als adäquat herausgestellt.
var curveLength = this.position.distanceTo(p1);
curveLength += p1.distanceTo(p2);
curveLength += p2.distanceTo(ship.position);
this.points = curve.getPoints(2 + Math.round(curveLength / (2 * this.speed * delta)));
this.points.shift();
Um nicht beim ersten Durchlauf einen Fehler zu erhalten, werden zwei Punkte sichergestellt. Dies hat bei der Größenordung der Punktanzahl keine gravierenden Auswirkungen. Initial wird der erste Punkt der Kurve entfernt, da es sich um die jetzige Position des Gegners handelt. Würde diese nicht entfernt werden, würde der Gegner ein Frame lang stehen bleiben.
Zu erwähnen ist das Verhalten bei höheren Geschwindigkeiten der Gegner und einer klein gewählten shipSize. Die shipSize kontrolliert den Abstand, der bestimmt, wie eng die Gegner an das Spielerschiff vorbeifliegen. Sind diese wie oben gewählt, beginnen die Gegner sich auch ohne den Austausch von Informationen in Formation zu begeben und verhalten sich ähnlich zu einem Vogelschwarm, der einem Hindernis ausweicht.